Menyembunyikan Rumus Excel 2007 Part II

Menyembunyikan rumus excel 2007 part II. Memang pada tulisan saya sebelumnya telah ada di Menyembunyikan rumus excel 2007, namun ada beberapa kekurangan. Yakni hanya bersifat read-only saja. Bedanya hanya dalam hal input data atau formula, maka data atau formula tersebut akan tetap berjalan sebagaimana fungsinya. Dan kebetulan beberapa waktu lalu ada seorang teman menelepon saya. Beliau menanyakan bagaimana sih cara menyembunyikan rumus rahasia pada Excel part II.

Berikut tips singkatnya :

1. Buka Microsoft Excel 2007 tentunya.

2. Blok seluruh cell, cara mudahnnya tekan tombol Ctrl+A

3. Format Cell > protection
hilangkan tanda cek pada lock, beri tanda cek pada Hidden

4. klik tools > protection > protect sheet > masukan pasword > ulangi pasword > ok

5. sim salaaa bim. rumus anda menjadi tersembunyi, serta anda dapat melakukan edit, input data atau rumus dengan tidak terlihat pada kotak formula.

Semoga Tutorial, Panduan merancang Formula atau Rumus Tips dan Trik dalam Belajar serta cara mengoptimalkan fungsi dasar Microsoft Excel 2007 untuk bisnis bermanfaat bagi anda. Jika ada pertanyaan, silahkan sampaikan sebisa dan secepat mungkin nanti akan saya tanggapi.

[Tutorial] Contoh Analisis Regresi Logistik biner/dikotomi dengan SPSS

Pada hari sebelumnya telah dibahas tentang konsep dari regresi logistik biner. Sesuai dengan janji penulis akan dibahas tutorial regresi logistik biner dengan SPSS. (kayak pemilu aja ya.:p). Untuk contoh kasus kali ini, terinspirasi dari tugas kelompok perkuliahan yang diambil dari tugas kakak tingkat. bisa dibilang copas lah ya. tapi, jangan dilihat dari copasnya. tapi lihat dari niatnya dan keinginan untuk saling berbagi semoga dapat membantu mengerjakan tugas, skripsi, tesis atau bahkan disertasi.

Contoh Kasus Analisis Regresi Logistik biner:

Dilakukan simulasi untuk melihat pengaruh antara variabel profitabilitas, kompleksitas perusahaan, opini auditor, likuiditas dan ukuran perusahaan terhadap ketepatan penyampaian laporan keuangan tahunan perusahaan. Profitabilitas diukur dengan ROA; variabel kompleksitas terdiri atas 2 kategorik yaitu diberi angka 2 jika mempunyai anak perusahaan dan 1 jika perusahaan tidak mempunyai anak perusahaan; opini auditor diukur dengan 2 jika mendapatkan opini wajar tanpa pengecualian dan 1 untuk opini yang lain; likuiditas diukur dengan Current Ratio; dan ukuran perusahaan diukur dengan logaritma natural market value. Variabel terikatnya adalah ketepatan penyampaian laporan keuangan, dengan kode 1 untuk perusahaan yang tepat waktu dan 0 untuk perusahaan yang terlambat.

Data yang digunakan dalam penelitian ini tidak ditampilkan mungkin kalau teman ingin mencoba juga bisa didownload dibagian bawah nanti ya. dalam tutorial ini menggunakan SPSS 20.Langsung saja ya dengan langkah-langkahnya.

Langkah-langkah dalam pengujian analisis regresi logistik

1. Pada posisi file telah terbuka, maka akan terlihat pada layar data tentang ketepatan penyampaian laporan keuangan perusahaan dengan sejumlah variabel-variabelnya. Untuk menganalisis, langkah awalnya adalah pilih menu Analyze, kemudian pilih Regression dan Binary Logistic. Maka akan muncul tampilan seperti di bawah ini.
   
2. Masukan variabel yang berfungsi sebagai variabel tak bebas dari box variabel ke kolom dependent, dan masukan semua varibel bebas pada kotak Covariate. Untuk Method, pilih Enter. Sebenarnya bisa dipilih metode apa saja karena model yang terbentuk akan sama (dalam artian penduga-penduga parameternya akan memiliki nilai-nilai yang sama). Akan tetapi, khusus metode Enter, harus dilakukan proses dua kali. Pertama, data di run dengan semua variabel untuk mengetahui variabel mana yang signifikan, setelah itu di run lagi dengan menggunakan variabel yang signifikan itu. Model yang terbentuk akan sama dengan model yang diperoleh dengan metode lain.
   
3. Klik Categorical, masukkan semua variabel bebas yang berbentuk kategori pada kotak covariate ke dalam kotak categorical covariates, biarkan contras pada default indicator. Untuk reference kategori pilih bagian kategori yang akan dipakai sebagai referensi atau pembanding yang akan digunakan dalam interpretasi odds ratio. Dapat menggunakan kategori akhir (last) atau kategori pertama (first). Dalam penelitian ini digunakan kategori akhir (last). Kemudian klik Continue. Setelah itu pilih menu option, centang iteration history untuk dapat mengetahui proses iterasi yang telah berlangsung.
   
4. Selain itu, akan ditemukan "Classification cut off", yang pada kondisi default sudah diisi dengan 0.5. Nilai ini disebut dengan the cut value atau prior probability, peluang suatu observasi untuk masuk ke salah satu kelompok sebelum karakteristik variabel penjelasnya diketahui. Jika kita tidak mempunyai informasi tambahan tentang data kita, maka kita bisa menggunakan default. Misalnya pada penelitian ini, sebelumnya tidak pernah dilakukan penelitian apakah ukuran perusahaan condong pada satu sisi. dengan alasan ini, dapat digunakan classification cutoff sebesar 0,5. Namun, misalnya pada ada penelitian lain yang telah meneliti maka bisa dinaikkan/diturunkan classification cutoff sesuai hasil penelitian. Dalam penelitian ini semua variabel numerik dalam default 0,5. Abaikan bagain yang lain, klik continue.
5. Abaikan bagian yang lain, dan tekan OK maka akan keluar output dari Regresi Logistik.

Intrepretasi Hasil analisis regresi logistik

Setelah keluar output dari hasil running data di SPSS maka diperoleh hasil analisis sebagai berikut :

Identifikasi Data yang Hilang

Pada tabel di atas, dapat dilihat tidak ada data yang hilang (missing cases).

Pemberian kode variabel respon oleh SPSS

Menurut pengkodean SPSS, yang termasuk kategori sukses adalah penyampaian laporan keuangan tahunan yang tepat.

Pemberian kode untuk variabel penjelas yang kategorik

Pengkodean variabel penjelas hanya dilakukan untuk variabel penjelas yang kategorik karena akan dibentuk dummy variabel. Penelitian ini menggunakan dua variabel penjelas yang kategorik yaitu variabel Opini dan variabel Kompleksitas. Untuk variabel opini, nantinya yang akan digunakan sebagai reference code (kode pembanding) adalah Wajar Tanpa Pengecualian (lihat pada tabel di atas bagian parameter codings yang berkode nol). Sementara untuk variabel Kompleksitas, yang menjadi kode pembanding adalah Punya anak perusahaan. Kode pembanding ini akan digunakan untuk interpretasi Odds Ratio.

Uji Signifikansi Model

Dari hasil SPSS dapat digunakan tabel “Omnibus Tests of Model Coefficients” untuk melihat hasil pengujian secara simultan pengaruh variabel bebas ini.

Berdasarkan tabel di atas diperoleh nilai Sig.Model sebesar 0.000. Karena nilai ini lebih kecil dari 5% maka kita menolak Ho pada tingkat signifikansi 5% sehingga disimpulkan bahwa variabel bebas yang digunakan, secara bersama-sama berpengaruh terhadap ketepatan penyampaian laporan keuangan suatu perusahaan. Atau minimal ada satu variabel bebas yang berpengaruh.

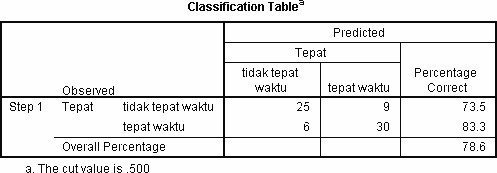
Persentase Ketepatan Klasifikasi (Percentage Correct)

Persentase ketepatan model dalam mengkasifikasikan observasi adalah 78.6 persen. Artinya dari 70 observasi, ada 55 observasi yang tepat pengklasifikasiannya oleh model regresi logistik. Jumlah observasi yang tepat pengklasifikasiannya dapat dilihat pada diagonal utama.

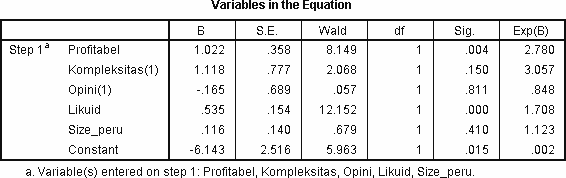
Uji Parsial dan Pembentukan Model

Pada uji diharapkan Ho akan ditolak sehingga variabel yang sedang diuji masuk ke dalam model. Dengan bantuan tabel “Variables in The Equation” dapat dilihat variabel mana saja yang berpengaruh signifikan sehingga bisa dimasukkan ke model. Jika nilai sig.<a maka Ho ditolak.

Berdasarkan hasil di atas diketahui bahwa terdapat 2 variabel bebas yang signifikan berpengaruh terhadap ketepatan penyampaian laporan keuangan perusahaan karena masing-masing variabel tersebut memiliki nilai signifikansi yang lebih kecil dari a=5%. Variabel-variabel tersebut adalah Profitabilitas (Sig.=0.004)dan Likuiditas (Sig.=0.000). Model yang terbentuk adalah :

Dimana :
X_1i = Profitabilitas
X_2i= Likuiditas
i=1,2,…,n

7.Interpretasi Odds Ratio

Nilai Odds ratio ini juga disediakan oleh tabel “Variables in The Equation” pada kolom Exp(B) :

Berdasarkan hasil di atas kita dapat menginterpretasikan Odds ratio sebagai berikut :

1. Jika jumlah profitabilitas perusahaan bertambah 1 unit maka kecendrungan perusahaan tersebut untuk tepat waktu menyampaikan laporan keuangan menjadi 2.780 kali lipat.
2. Sebuah perusahaan yang tidak mempunyai anak perusahaan akan memiliki kecenderungan untuk menyampaikan laporan keuangan secara tepat waktu sebesar 3.057 kali dibanding perusahaan yang memiliki anak perusahaan (merujuk pada reference code).
3. Perusahaan dengan opini auditor adalah opini lain cenderung 0.848 kali (lebih rendah) untuk tepat waktu dalam menyampaikan laporan keuangan dibanding dengan perusahaan yang Wajar tanpa Pengecualian.
4. Jika Current ratio pada likuiditas bertambah 1 persen maka perusahaan akan cenderung 1.708 kali untuk tepat waktu menyampaikan laporan keuangannya.
5. Ketika ukuran perusahaan bertambah 1 unit maka perusahaan tersebut cenderung 1.123 kali untuk tepat waktu dalam menyampaikan laporan keuangannya.

Buat yang ingin mencoba silahkan download filenya dibawah ini:
tutorial reglog biner (SPSS 20)

Konsep Regresi Logistik Biner/Dikotomi

Analisis regresi logistik merupakan metode analisis yang biasanya digunakan oleh mahasiswa dalam menyelesaikan skripsi berkaitan dengan skripsi tentang persepsi. bahasa gaul metode ini biasa disebut reglog. Untuk pembahasan kali akan dibahas materi reglog dulu. dan akan dilakukan untuk contoh kasusnya dengan software SPSS. Mudah-mudahan bisa membantu para cendikiawan muda termasuk penulis sendiri.hehehhe

Analisis regresi logistik digunakan untuk menjelaskan hubungan antara variabel respon yang berupa data dikotomik/biner dengan variabel bebas yang berupa data berskala interval dan atau kategorik (Hosmer dan Lemeshow, 1989). Variabel yang dikotomik/biner adalah variabel yang hanya mempunyai dua kategori saja, yaitu kategori yang menyatakan kejadian sukses (Y=1) dan kategori yang menyatakan kejadian gagal (Y=0). pada model model linear umum komponen acak tidak harus mengikuti sebaran normal, tapi harus masuk dalam sebaran keluarga eksponensial. Sebaran bernoulli termasuk dalam salah satu dari sebaran keluarga eksponensial. Variabel respon Y ini, diasumsikan mengikuti distribusi Bernoulli.

Timbul pertanyaan:Perbedaan antara regresi logistik dengan analisis regresi biasa? kenapa tidak pakai analisis regresi biasa aja?

Sebenarnya untuk masalah diatas bisa digunakan analisis regresi OLS. Tapi harus memenuhi asumsi bahwa 0 <= E(Yi ÷ Xi) <= 1. Namun persyaratan tersebut sulit untuk terpenuhi. sehingga metode regresi OLS kurang cocok untuk data kuantitatif dan lebih baik menggunakan metode regresi logistik.

contoh Kasus dalam regresi logsitik biner:

1. Pengaruh Tingkat Pendidikan, Lapangan Kerja yg dimasuki, Pendapatan, Pengeluaran, Jumlah ART terhadap status kemiskinan (Miskin/TIdak Miskin).
2. Pengaruh Pendapatan Keluarga, Banyaknya Anggota Keluarga, Jenis rumah, Usia Kepala Keluarga terhadap Kepemilikan rumah (Punya rumah/tidak)

Berdasarkan dua contoh tersebut mungjkin sudah membuka pikiran untuk kasus seperti apa regresi logistik digunakan. intinya variabel dependentnya dikotomi artinya memiliki dua kategori seperti pada kasus diatas yang ditebal.

Kenapa cuma dua kategori aja? tidak bisa lebih dari tiga kategori?

Untuk metode ini tidak bisa karena hanya bisa dua sesuai dengan namanya. untuk masalah diatas ada metode lain yang bisa digunakan yaitu regresi logistik ordinal.

Bagaimana langkah-langkah atau prosedur statistiknya? sebagai referensi buat skripsi.hehehe

Bentuk umum model peluang regresi logistik dengan p variabel penjelas, diformulasikan sebagai berikut:

dengan π(x) adalah peluang kejadian sukses dengan nilai probabilita 0≤π(x)≤1 dan βj adalah nilai parameter dengan j = 1,2,......,p. π(x) merupakan fungsi yang non linier, sehingga perlu dilakukan transformasi ke dalam bentuk logit untuk memperoleh fungsi yang linier agar dapat dilihat hubungan antara variabel bebas dan variabel tidak bebas. Dengan melakukan transformasi dari logit π(x), maka didapat persamaan yang lebih sederhana, yaitu:

Jika dari beberapa variabel bebas ada yang berskala nominal atau ordinal, maka variabel tersebut tidak akan tepat jika dimasukkan dalam model logit karena angka-angka yang digunakan untuk menyatakan tingkatan tersebut hanya sebagai identifikasi dan tidak mempunyai nilai numerik dalam situasi seperti ini diperlukan variabel dummy. Untuk variabel bebas dengan skala ordinal maupun nominal dengan k kategori, akan diperlukan sebanyak k-1 variabel dummy.

Asumsi-asumsi dalam regresi logistik:

• Tidak mengasumsikan hubungan linier antar variabel dependen dan independent
• Variabel dependen harus bersifat dikotomi (2 variabel)
• Variabel independent tidak harus memiliki keragaman yang sama antar kelompok variabel
• Kategori dalam variabel independent harus terpisah satu sama lain atau bersifat eksklusif
• Sampel yang diperlukan dalam jumlah relatif besar, minimum dibutuhkan hingga 50 sampel data untuk sebuah variabel prediktor (bebas).

Pendugaan Parameter

Metode untuk mengestimasi parameter-parameter yang tidak diketahui dalam model regresi logistik ada 3 yaitu:
1. Metode kemungkinan maksimum (Maximum Likelihood Method)
2. Metode kuadrat terkecil tertimbang noniterasi (Noniterative Weight Least Square Method)
3. Analisis fungsi diskriminan (Discriminant Fuction Analysis)

Pada dasarnya metode maksimum Likelihood merupakan metode kuadrat terkecil tertimbang dengan beberapa proses iterasi, sedangkan metode noniterative weight least square method hanya menggunakan satu kali iterasi. kedua metode ini asymptoticaly equivalent, artinya jika ukuran sampel besar keduanya akan menghasilkan estimator yang identik. Penggunaan fungsi diskriminan mensyaratkan variabel penjelas yang kuantitatif berdistribusi normal. Oleh karena itu, penduga dari fungsi diskriminan akan over estimate bila variabel penjelas tidak berdistribusi normal.

Dari Ketiga metodei di atas, metode yang banyak digunakan adalah metode maksimum likelihood dengan alasan lebih praktis (Nachrowi dan Usman, 2002). Metode maksimu likelihoood ini menduga parameter dengan nilai yang memaksimumkan fungsi likelihood (likelihood function).

Uji Signifikansi Model

Untuk mengetahui pengaruh variabel bebas terhadap variabel tidak bebas secara bersama-sama (overall) di dalam model, dapat menggunakan Uji Likelihood Ratio. Hipotesisnya adalah sebagai berikut:
Ho: β1 = β2 =....= βp = 0 (tidak ada pengaruh veriabel bebas secara simultan terhadap variabel tak bebas)
H1: minimal ada satu βj ≠ 0 (ada pengaruh paling sedikit satu veriabel bebas terhadap variabel tak bebas)
Untuk j = 1,2,...,p
Statistik uji yang digunakan adalah:

Dengan :

Lo = Maksimum Lieklihood dari model reduksi (Reduced Model) atau model yang terdiri dari konstanta saja

Lp = Maksimum Likelihood dari model penuh (Full Model) atau dengan semua variabel bebas.

Statistik G2 ini mengikuti distribusi Khi-kuadrat dengan derajad bebas p sehingga hipotesis ditolak jika p-value < α, yang berarti variabel bebas X secara bersama-sama mempengaruhi variabel tak bebas Y.

Uji Parsial dan Pembentukan Model

Pada umumnya, tujuan analsis statistik adalah untuk mencari model yang cocok dan keterpautan yang kuat antara model dengan data yang ada. Pengujian keberartian parameter (koefisien β) secara parsial dapat dilakukan melalui Uji Wald dengan hipotesisnya sebagai berikut:

Ho: βj = 0 (variabel bebas ke j tidak mempunyai pengaruh secara signifikan terhadap variabel tidak bebas)
H1: βj ≠ 0 (variabel bebas ke j mempunyai pengaruh secara signifikan terhadap variabel tidak bebas)
Untuk j = 1,2,....,p

Dengan statistik uji sebagai berikut:

Hipotesis akan ditolak jika p-value < α yang berarti variabel bebas Xj secara partial mempengaruhi variabel tidak bebas Y.

Odds Ratio

Odds ratio merupakan ukuran risiko atau kecenderungan untuk mengalami kejadian ‘sukses ‘ antara satu kategori dengan kategori lainnya, didefinisikan sebagai ratio dari odds untuk xj = 1 terhadap xj = 0. Odds ratio ini menyatakan risiko atau kecenderungan pengaruh observasi dengan xj = 1 adalah berapa kali lipat jika dibandingkan dengan observasi dengan xj = 0. Untuk variabel bebas yang berskala kontinyu maka interpretasi dari koefisien βj pada model regresi logistik adalah setiap kenaikan c unit pada variabel bebas akan menyebabkan risiko terjadinya Y = 1, adalah exp(c.βj) kali lebih besar.

Odds ratio dilambangkan dengan θ, didefinisikan sebagai perbandingan dua nilai odds xj = 1 dan xj = 0, sehingga:

Silahkan klik link berikut Tutorial regresi logistik dengan SPSS