Contoh kasus arima box-jenkins
contoh kasus kali ini menggunakan data ihsg selama 48 hari. data yang digunakan hanya fiktif saja. tujuan dari analisis ini untuk menentukan model terbaik yang bisa digunakan untuk peramalan. berikut data yang digunakan.| Hari | IHSG | Hari | IHSG | Hari | IHSG | Hari | IHSG | Hari | IHSG | Hari | IHSG | Hari | IHSG | Hari | IHSG |
| 1 2 3 4 5 6 | 240 240 240 220 210 150 | 7 8 9 10 11 12 | 230 230 250 200 190 170 | 13 14 15 16 17 18 | 220 180 320 320 270 220 | 19 20 21 22 23 24 | 220 190 190 180 270 300 | 25 26 27 28 29 30 | 230 200 200 290 290 270 | 31 32 33 34 35 36 | 270 230 260 240 180 170 | 37 38 39 40 41 42 | 150 140 210 330 350 350 | 43 44 45 46 47 48 | 210 260 210 340 300 290 |
Flowchart dalam Arima box-jenkins
Sebelum memulai saya akan memberikan flowchart sebagai gambaran umum langkah-langkah yang harus dilakukan sehingga mempermudah pemahaman awal. sehingga seterusnya bisa dimengerti langkah-langkah dibawah ini.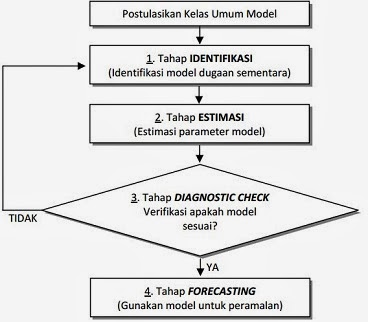
Langkah-langkah dalam analisis arima box-jenkins
Import data
- Buka workfile baru dengan cara File > New > Workfile. Maka akan muncul tampilan seperti berikut yang digunakan untuk menentukan deskripsi data.
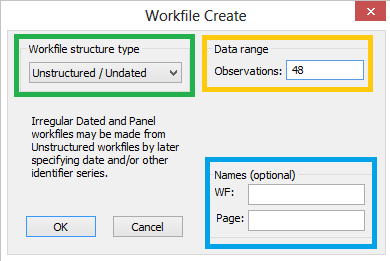
- Workfile structure type : digunakan untuk menetukan struktur data. ada 3 jenis struktur:
- unstructured/undated : tidak struktur atau tidak ditentukan waktunya untuk data time series.
- Dated : menentukan waktu data untuk data time series.
- Balanced panel : menentukan data untuk data panel.
- Date range: Deskripsi dari struktur data yang terpilih tadi. ini akan berubah tergantung dari tipe struktur yang terpilih. untuk yang undated isi dengan banyaknya observasi.
- Name(optional) : untuk memberi nama workfile dan nama page. ini hanya optional.
- setelah itu akan muncul tampilan berikut.
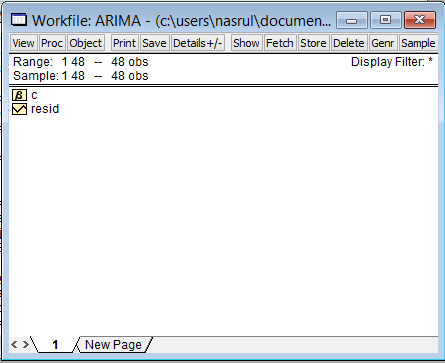
- Masukkan/import data series yang terdapat pada file ihsg arima.xls dalam Workfile di EViews. Caranya pilih File > Import > Read text-Lotus-Excel. kemudian pilih data maka muncul jendela seperti berikut.
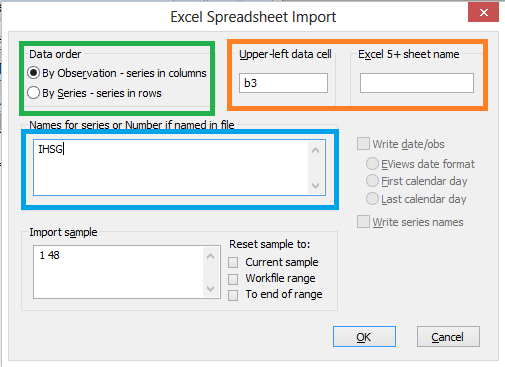
- Data order: menetukan data yang excel berada dalam satu baris atau satu kolom.
- Upper-left data cell: menetukan data cell(posisi) untuk data pertama yang berada di excel. kalau data berdasarkan kolom yang paling atas kalau data berdasarkan baris yang paling kiri
- Excel 5+ sheet name untuk menentukan sheet yang digunakan di excel. kalau menggunakan sheet default bisa dikosongkan saja.
- Names: isikan nama data
- maka akan muncul tampilan data yang digunakan. proses memasukkan data sudah selesai
Identifikasi Model
- Untuk menentukan model arima (p,d,f). awalnya kita menentukan nilai d dengan uji stasioneritas terlebih dulu. untuk langkah ini saya buat secara terpisah. jadi bisa buka link ini uji stasioneritas.
- jika sudah stasioner sudah cukup. Jika dianggap data belum stasioner, maka kita perlu melakukan differencing untuk menjadikan data stasioner. bisa dengan ganti di uji stasioner dengan level kemudian ganti dengan 1st difference atau 2nd difference pada uji stasioneritas tadi. Tujuan dari uji staasioner untuk menentukan pada saat kapan data stasioner yang digunakan untuk menentukan d pada model arima(p,d,f).
- level: d=0
- 1st difference: d=1
- 2nd difference: d=2
- dst
dalam contoh ini data stasioner pada level sehingga d=0. - Langkah berikutnya adalah menentukan p dan q untuk parameter ARIMA dengan cara melihat pola fungsi autokorelasi(ACF) dan autokorelasi parsial(PACF) dari data series. Untuk itu melalui menu Quick pilih Series Statistics > Correlogram sehingga tampil kotak dialog seperti pada Gambar di bawah.
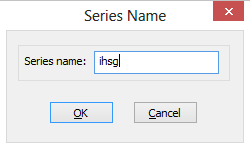
- Pada kotak Series name isikan nama series, yaitu ihsg, pilih level, kemudian klik OK. Berikutnya akan ditampilkan kotak dialog seperti pada Gambar berikut:
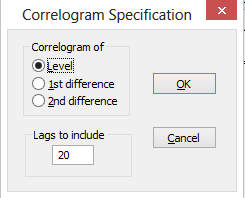
- Setelah klik OK, maka akan ditampilkan plot autokorelasi dan autokorelasi parsial sebagai berikut:

- dari plot autokorelasi(ACF) dan plot autokorelasi parsial(PACF), terlihat bahwa kedua gambar mengalami cutoff(turun drastis) pada baris pertama seperti ditunjukkan pada kotak hijau. Untuk penjelasan lengkap jika ada yang bentuknya berbeda silahkan kesini materi arima.
- jika cutoff pada ACF dan PACF maka kemungkinan pertama p=1 dan q=0 kemudian kemungkinan kedua p=0 dan q=1. sehingga jika digabung dengan d yang sudah diketahui nilainya. maka kemungkinan ARIMA(p,d,f) adalah ARIMA(1,0,0) bisa disingkat AR(1) atau model ARIMA(0,0,1) bisa disingkat MA(1).
Estimasi Model
- pada ARIMA kita menggunakan trial dan error untuk menentukan model terbaik. sehingga dilakukan estimasi untuk keduanya. contoh dibawah ini menggunakan kemungkinan pertama yaitu p=1,d=0 dan q=0 atau AR(1)
- langkah selanjutnya adalah pilih Quick > estimate equation. sehingga akan diperoleh dialog berikut.
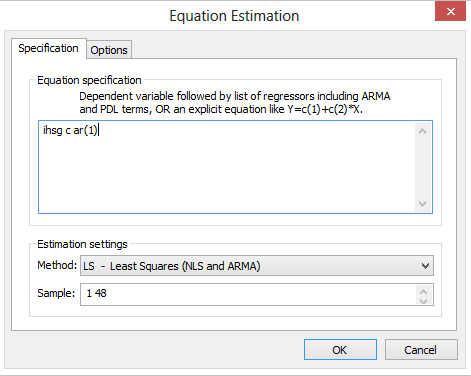
- pada equation specification untuk diisi dengan urutan seperti gambar diatas berikut penjelas:
- ihsg : sebagai nama data yang digunakan, tinggal diganti jika namanya beda. kemudian jika pada model yang digunakan d lebih besar dari 1. tinggal ditambahkan d(). contoh untuk d=1 maka menjadi d(ihsg), jika d=2 maka menjadi d(d(ihsg)), dst.
- c : sebagai konstanta, setelah nama data harus diisi c sebagi konstanta,
- ar(1) : sebagai nilai p,q tdi. ar menyatakan nilai p dan ma menyatakan nilai q. untuk kemungkinan pertama dimana p=1 dan q=0 maka menjadi ar(1)ma(0). tapi karena nilai ma=0 maka dihapus saja jadi tinggal ar(1).
- Setelah itu klik ok, maka akan muncul hasil seperti berikut.
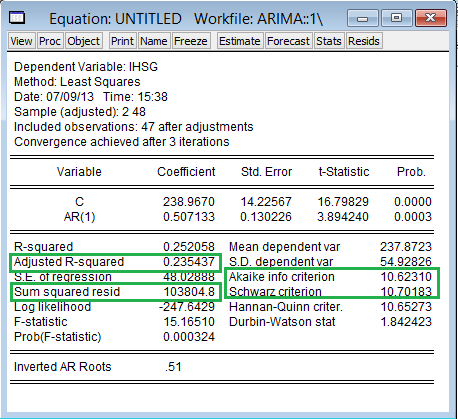
Lakukan untuk kemungkinan kedua. sudah tahu kan apa yang harus diisi pada equation specification. yup seperti ini. ihsg c ma(1).
Diagnosa Model
Setelah menduga parameter, langkah selajutnya adalah menguji kedua model apakah modelnya sudah baik untuk digunakan. Untuk melihat model yang baik bisa dilihat dari residualnya. Jika residualnya white noise, maka modelnya dapat dikatakan baik dan sebaliknya. Salah satu cara untuk melihat white noise dapat diuji melaluikorelogram ACF dan PACF dari residual. Bila ACF dan PACF tidak signifikan, ini mengindikasikan residual white noise artinya modelnya sudah cocok. jika tidak maka model tidak cocok.Caranya dengan pilih View > Residual tests > Correlogram-Q- Statistic. maka akan muncul output seperti berikut.

Interpretasi dari hasil diatas. terlihat bahwa prob. terdapat nilai yang signifikan artinya lebih kecil dari 0,05(alpha) pada beberapa lag. sehingga bisa dikatakan model tidak cocok. tapi untuk beberapa lag kemudian menunjukkan tidak signifikan walaupun begitu sepemahaman saya tetap tidak cocok. dalam menggunakan minitab untuk arima dalam outputnya menggunakan beberapa lag tertentu saja hanya lag 12, 24, 36 dan 48 yang dicantumkan sehingga apabila dicoba dengan minitab mungkin bisa memenuhi.Insya allah akan dibuatkan tutorial dengan minitab pada arima. Dalam contoh ini uji diagnostiknya diasumsikan terpenuhi sehingga kedua model lolos untuk uji diagnostik sehingga langkah selanjutnya memilih model terbaik diantara kedua model.
Pemilihan model terbaik
Ada beberapa kriteria dalam memilih model terbaik:- Nilai Schwarz criterion yang kecil
- Nilai Akaike info criterion (AIC) yang kecil
- SSE yang kecil
- Adjusted R squared yang besar
| Model | AIC | SBC | SSE | adj. R squared |
| AR(1) | 10,6231 | 10,70183 | 103804,8 | 23,5437 |
| MA(1) | 10,6644 | 10,74196 | 110634,6 | 18,5544 |
Setelah dilihat hasilnya diperoleh bahwa model terbaik adalah AR(1) karena memenuhi dari kriteria di atas .
No comments:
Post a Comment