Uji chi squared untuk uji kecocokan/ goodness of fit test

Uji chi squared secara yang dipernah dibahas pada postingan sebelumnya. salah satu kegunaan uji chi squared yaitu uji kecocokan atau goodness of fit test. silahkan klik link berikut untuk melihat penjelasan secara umum. Uji chi squared. Secara khusus akan dibahas untuk goodness of fit test beserta contoh kasus supaya lebih mudah dimengerti.

Uji kecocokan atau goodness of fit test, hipotesis nol merupakan suatu ketentuan tentang pola yang diharapkan dari frekuensi-frekuensi dalam kategori (-kategori) tertentu. Pola yang diharapkan harus sesuai dengan asumsi atau anggapan atas kemungkinan kejadian yang sama dan bersifat umum.

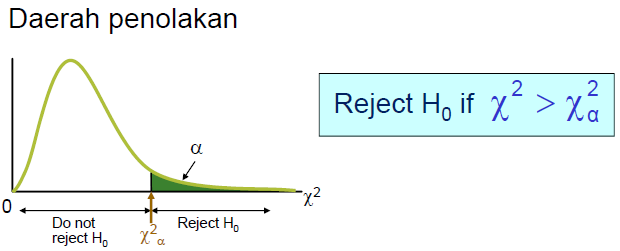
UJI KECOCOKAN (goodness of fit), membandingkan antara Frekuensi Observasi dengan Frekuensi Teoretis /Harapan. Apakah Frekuensi hasil Observasi menyimpang dari Frekuensi Harapan. Jika nilai (chi square) kecil, berarti kedua frekuensi tersebut sangat dekat, mengarah pada penerimaan kepada hipotesa nol (Ho).

Penetapan Hipotesis Awal dan Hipotesis Alternatif

H0 : frekuensi setiap kategori memenuhi suatu nilai/perbandingan.
H1 : Ada frekuensi suatu kategori yang tidak memenuhi nilai/perbandingan tersebut.

Penetapan Derajat Kebebasan (df)

Dalam uji kecocokan model derajad kebebasan (df) sama dengan jumlah kategori dikurangi jumlah estimator yang didasarkan pada sampel dan dikurang 1. Yang dimaksud estimator parameter adalah parameter yang diperkirakan nilainya, karena nilai parameter tidak dapat secara tepat ditentukan berdasarkan data sampel yang tersedia. Jika dirumuskan menjadi:
df = k – m -1
dengan :
k : jumlah kategori data sampel
m : jumlah nilai-nilai parameter yang diestimasi

Contoh Kasus uji kecocokan/ goodness of fit test

Sebuah distibutor alat penggilingan padi membagi pasar menjadi 4 wilayah (A, B, C, dan D). Ada informasi bahwa pendistribusian alat penggilingan merata pada setiap wilayah. Untuk membuktikan pernyataan tersebut diambil 40 arsip sebagai sampel. Dari 40 arsip tersebut diperoleh informasi yang tertuang dapa tabel. Gunakan tingat signifikansi 5 persen untuk menguji hipotesis yang menyatakan bahwa distribusi alat penggilingan di keempat wilayah merata (sama)

	Wilayah				Total Baris
	A	B	C	D
Data berdasarkan hasil sampel (O)	6	12	14	8	40
Data yang diharapkan (E)	10	10	10	10	40

Pembahasan Contoh goodness of fit

1. Hipotesis

Sebelum memulai pembahasan langkah pertama yang harus diketahui adalah permasalahan dan tujuan dari soal yang ingin dicapai oleh peneliti. Pertama Peneliti ingin membuktikan bahwa pendistribusian sama rata. sehingga bisa memperkirakan hipotesis. ini hipotesis yang digunakan dalam penelitian ini

Ho : distribusi alat penggilingan di keempat wilayah merata (sama)
Ha : distribusi alat penggilingan di keempat wilayah tidak merata (tidak sama)

2. Nilai Kritis

Kedua yang perlu diperhatikan yaitu nilai kritis. Maksud dari nilai kritis tersebut adalah nilai batas dari penentu keputusan hipotesis mana yang di ambil. sehingga ini sangat perlu dilakukan. Berdasarkan penjelasan di atas.  Dalam kasus di atas tidak perlu ada parameter yang diestimasi. oleh karena itu:

df = k – 1 = 4 – 0 – 1 = 3

k = jumlah kategori data sampel (A, B, C, dan D)

Selain itu tingkat signifikansi yang digunakan adalah 0,05(5%), sehingga nilai kritisnya adalah:

X₂(0,05;3) = 7,81

nilai 7,81 ini diperoleh dari tabel chi squared. untuk mengetahui nilai tersebut harus punya tabel chi squared. silahkan klik link berikut jika mau lihat tabel chi squared

3. Nilai Hitung

Nilai uji statistik X₂ hitung diperoleh dengan cara sebagai berikut seperti pada materi sebelumnya dalam uji chi squared:

4. Kesimpulan

Setelah diperoleh nilai statistik hitung yaitu 4. kemudian kita bandingkan dengan nilai kritis tadi yang sudah diperoleh sebelumnya yaitu 7,81. nilai statistik hitung lebih kecil dari nilai kritis hitung maka keputusan tidak menolak H0, sehingga keputusan yang diperoleh berdasarkan H0 yaitu distribusi alat penggilingan di keempat wilayah merata (sama). Sudah mengerti kan ya? Bagaimana kalau nilai statistik hitung lebih besar dari nilai kritis maka keputusannya sebalikknya yaitu berdasarkan hasil Hipotesis alternatif (Ha).

Cara mengisi sel pada sheet yang terprotect

setiap orang tentunya ingin agar rumus pada database tidak diketahui orang lain. berawal dari komentar seorang pembaca setia dari sobat @infoexcel07 mengenai komentar kang Idrus Muhammad pada tulisan cara proteksi cell, sheet dan workbook pada excel 2007. kali ini info excel akan memberikan jawaban mengenai pertanyaan untuk dapat Cara mengisi sel pada sheet yang terprotect. semoga dapat memberikan jawaban yang maksimal dikarenakan akhir-akhir ini admin lagi sakit batuk dan panas alias meriyang, jadi harap maklum ya klo jawabnya agak lama.

trik yang sederhana sehingga tetap terlindungi untuk password yang memang dirahasiakan. berikut langkah singkatnya.

1. blok area yang menjadi input / masukan yang akan dirubah. diharapkan agar bukan rumus yang di blok ya karena Nantinya, kursor hanya akan berada pada area yang diblok saja. jadi, untuk rumusnya harap sudah dipatenkan terlebih dahulu sebelum dilakukan trik protect password.

2. klik kanan pada area yang sudah di blok atau diseleksi, lalu pilih format cell. dapat juga dengan menekan shorcut pada keyboard ctrl+1

3. kemudian pilih tab properties, hilangkan tanda locked. akhiri dengan menekan tombol OK.

4. klik kanan pada nama sheet, pilih protect sheet. nah, disini kunci utamanya agar dapat memilih sel yang dapat diutak-atik atau diubah-ubah atau juga di edit-edit untuk isinya.

5. cek pada select unlocked cells dan edit objects. klik ok untuk mengeksekusi perintah tadi. jangan lupa juga masukkan passwordnya dua kali dengan pasword yang sama yah agar perintah tadi dapat bekerja.

6. taraaa, sel yang sebelumnya di pilih dan akan di edit-edit akan bisa diubah tanpa masalah.

apabila belum dapat melakukan trik Cara mengisi sel pada sheet yang terprotect, diharapkan untuk memperhatikan langkah demi langkah sehingga trik Cara mengisi sel pada sheet yang terprotect dapat bekerja dengan maksimal dan rumus anda tetap menjadi rahasia dengan aman terkendali. selamat mencoba ya teman @infoexcel07.

uji chi squared

Setelah sebelumnya sudah membahas tentang materi umum non parametrik. kali ini akan menjelaskan salah satu dari uji non parametrik. Postingan kali ini membahas mengenai uji chi-square. Sedikit berbeda dengan sebelumnya, Saya  mencoba memulai dengan contoh agar lebih mudah dipahami. Mudah-mudahan lebih ngerti ya, kalau belum ngerti di komen yaaa.

Contoh uji chi square : Sebuah dadu setimbang dilempar sekali 120 kali,di peroleh data sebagai berikut.sisi 1 = 20, sisi 2 = 22, sisi 3 = 17, sisi 4 = 18, sisi 5 = 19 dan sisi 6 = 24. Dari hasil tersebut kita ingin lihat apakah hasi lemparan tersebut masuk akal. maksud dari masuk akal peluang muncul ke enam sisi tersebut sama 120/6 = 20. jadi, kita pengen tahu apakah lemparan itu masuk akal.

Contoh di atas merupakan salah satu contoh penggunaan uji chi-square. pertanyaannya pasti kenapa? disini kita melakukan observasi (melempar dadu) sebanyak 120 kali. terus kita ingin membuktikan secara ilmiah apakah hasil observasi sesuai dengan perkiraan (Harapan) yaitu peluang muncul ke enam sisi sama.
Intinya membandingkan hasil obesravasi dengan harapan yang seharusnya.

Kesimpulannya Uji chi-square merupakan pengujian hipotesis tentang perbandingan antara frekuensi sampel yang benar-benar terjadi (selanjutnya disebut dengan frekuensi observasi – O) dengan frekuensi harapan yang didasarkan pada hipotesis tertentu pada setiap kasus atau data (selanjutnya disebut dengan frekuensi harapan – E).

Setelah kita mengetahui bagaimana uji chi square, sekarang kita perlu mengetahui distribusi dari uji chi square. distribusi chi square ini lah yang digunakan dalam uji ini. sehingga yang menentukan apakah ada perbedaaan atau tidak ya distribu chi squared. Distribusi khi-kuadrat yang kita gunakan sebagai uji statistik mempunyai karakteristik sebagai berikut:

1. Nilai Khi-kuadrat tidak pernah negatif, karena selisih dari frekuensi pengamatan dan frekuensi harapan dikuadratkan.
2. Ketajaman dari distribusi khi-kuadrat tidak tergantung pada ukuran sampel tetapi tergantung pada banyaknya kategori yang digunakan.
3. Distribusi khi-kuadrat bersifat menceng kanan (nilai positif), semakin meningkat jumlah derajat bebas maka semakin mendekati distribusi normal.

Sebagai rumus dasar dari uji Chi Square adalah sebagai berikut:

Sedangkan untuk mendapatkan frekuensi yang diharapkan ada dua cara. pertama frekuensi harapan sudah diketahui seperti contoh di atas kemudian cara kedua dengan menggunakan rumus tapi ini berlaku untuk data yang sudah ditabulasi. nanti akan diberikan contoh. rumusnya seperti berikut.

Langkah-langkah/ prosedur dalam uji chi squared secara umum 

1. Letakkan frekuensi-frekuensi terobservasi dalam k kategori. Jumlah frekuensi itu seluruhnya harus N, yakni banyak observasi-observasi independen.
2. Dari H0 tentukan frekuensi yang diharapkan untuk tiap-tiap k sel itu. Manakala k>2, dan bila lebih dari 20% dari Ei kurang dari 5, gabungkanlah kategori-kategori yang berdekatan apabila hal ini memungkinkan, dan dengan demikian kita mengurangi harga k serta meningkatkan nilai beberapa Ei. Apabila k=2, tes X² untuk kasus satu sampel dapat digunakan secara memadai hanya jika tiap-tiap frekuensi yang diharapkan adalah lima atau lebih.
3. Hitung nilai X2 dengan rumus Σ(Oi-Ei)2/Ei.
4. Tetapkan harga db=k-1.
5. Dengan melihat tabel Chi squared, tetapkan probabilitas yang dikaitkan dengan terjadinya suatu harga yang sebesar nilai X² hitungan untuk harga db yang bersangkutan. Jika nilai ini sama atau kurang dari α, H0 ditolak.

Uji Chi Square dapat digunakan untuk menguji :

1. Uji X² untuk Bentuk Distribusi (Goodness of Fit)
   UJI KECOCOKAN (goodness of fit), membandingkan antara Frekuensi Observasi dengan Frekuensi Teoretis /Harapan. Apakah Frekuensi hasil Observasi menyimpang dari Frekuensi Harapan. Jika nilai (chi square) kecil, berarti kedua frekuensi tersebut sangat dekat, mengarah pada penerimaan kepada hipotesa nol ( Ho).
2. Uji X² untuk Independensi
   UJI INDEPENDENSI : Menguji apakah ada atau tidak ada hubungan antara dua kategori suatu hasil observasi dari suatu populasu dnegan kategori populasi lainnya. Uji independensi disebut juga analisis tabel kontingensi
3. Uji X² untuk Perbedaan
   Uji chi squared untuk perbedaan: Bentuk hipotesis (Ho) yang digunakan dalam hal ini adalah: “tidak terdapat perbedaan dari keadaan atau peristiwa dari kelompok sampel yang satu dengan kelompok sampel yang lain”. Sedangkan untuk Ha adalah: “terdapat perbedaan dari keadaan atau peristiwa dari kelompok sampel yang satu dengan kelompok sampel yang lain”.

Selanjutnya akan dibahas secara terperinci dari ketiga jenis uji chi squared di atas. Sampai ketemu di pertemuan selanjutnya. Kalau ada yang butuh tabel chi squared silahkan kesini.