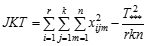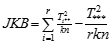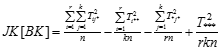Contoh Kasus Anova dua arah dengan interaksi:
Terdapat 4 metode diet, 3 kelompok umur dan 3 ulangan. Berikut adalah data rata-rata penurunan berat badan setelah 1 bulan melakukan diet. Ujilah apakah penurunan berat badan sama untuk setiap metode diet, kelompok umur dan interaksi dengan taraf uji 5 %?| Umur | Penurunan Berat Badan (Kg) | Total Baris | |||
| Metode 1 | Metode 2 | Metode 3 | Metode 4 | ||
| < 20 tahun #1 #2 #3 | 5 4 5 | 0 2 1 | 3 4 8 | 4 2 2 | T1** = 40 |
| T11* = 14 | T12* = 3 | T13* = 15 | T14* = 8 | ||
| 20-40 tahun #1 #2 #3 | 5 6 2 | 4 2 1 | 2 2 4 | 5 3 2 | T2**=38 |
| T21* = 13 | T22* = 7 | T23* = 8 | T24* = 10 | ||
| > 40 tahun #1 #2 #3 | 4 4 5 | 5 5 0 | 2 1 2 | 6 4 4 | T3**=42 |
| T31* = 13 | T32* = 10 | T33* = 5 | T34* = 14 | ||
| Total Kolom | T*1* = 40 | T*2* = 20 | T*3* = 28 | T*4* = 32 | Total T***=120 |
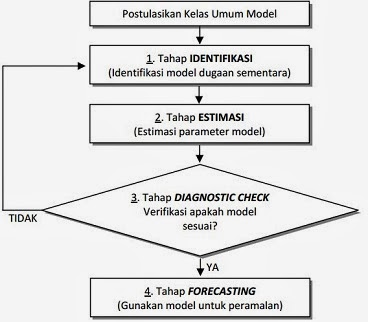
Solusi kasus Anova dua arah dengan interaksi
Identifikasi Metode statistik yang digunakan
Pertama. berdasarkan hipotesis yang digunakan yaitu membandingkan rata-rata lebih dari dua kelompok maka metode yang mungkin adalah Anova. kedua Sampel yang digunakan tiap kelompok sudah dikategorikan sehingga tipe anova yang cocok adalah Anova dua arah. kemudian dari tiap kategori tersebut ada pengulangan sehingga kita menggunakan anova dua arah dengan interaksi.Dalam metode anova yang perlu diperhatikan ada empat. asumsi normal dan homogenitas antar varians kelompok harus terpenuhi. dalam contoh ini kita asumsikan asumsi terpenuhi karena kita fokus pada langkah-langkah anova dua arah dengan interaksi. kemudian kelompok yang dianalisis berasal dari kelompok saling bebas. dan data yang digunakan merupakan data rasio. Setelah asumsi ini terpenuhi maka bisa lanjut ke perhitungan selanjutnya. kalau tidak ganti metode.
Pada anova dua arah dengan interaksi terdapat tiga hipotesis yang digunakan sehingga nanti :
- Hipotesis anova kolom
H0: µ*1 = µ*2 = µ*3, Tidak ada perbedaan yang nyata antara rata-rata hitung dari kategori Metode
H1: µ*1 ≠ µ*2 ≠ µ*3, Ada perbedaan yang nyata antara rata-rata hitung dari kategori Metode - Hipotesis anova baris
H0: µ1* = µ2* = µ3*, Tidak ada perbedaan yang nyata antara rata-rata hitung dari kategori kelompok umur
H1: µ1* ≠ µ2* ≠ µ3*, Ada perbedaan yang nyata antara rata-rata hitung dari kategori Kelompok umur - Hipotesis interaksi
H0: (ab)11 = (ab)12 = ... = (ab)kj, Tidak ada interaksi antara variabel metode dan umur
H1: (ab)11 ≠ (ab)12≠ ... ≠(ab)kj, ada interaksi antara variabel metode dan umur
Langkah-langkah dalam uji hipotesis anova dua arah dengan interaksi
- Load Package Rcmdr. Hal ini dilakukan karena paket yang digunakan dalam R adalah R commander. Caranya klik Packages kemudian pilih Load package terus muncul tampilan dan pilih Rcmdr. Untuk yang belum punya silahkan kesini buat jelasnya.
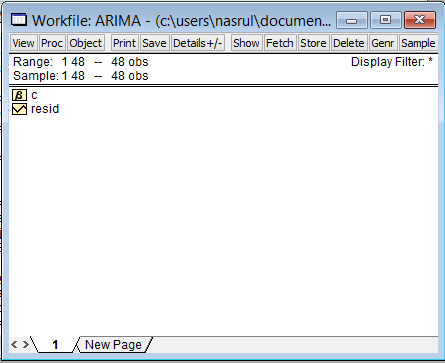
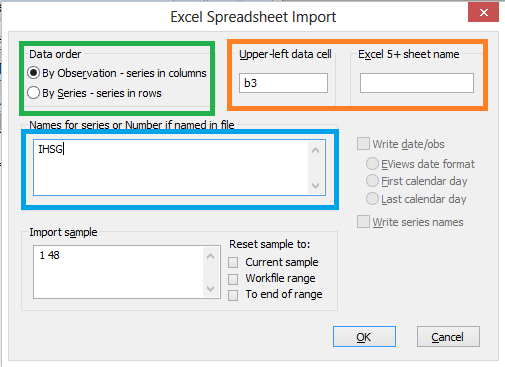
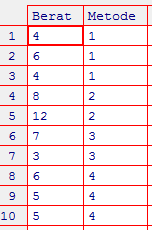
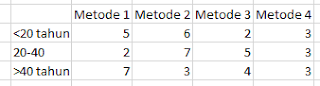
- Masukkan data. Caranya yaitu buat dua kolom yang pertama berupa semua nilai. kedua yaitu kolom yang menyatakan penjelasan kelompok dari kolom pertama. untuk lebih jelasnya berikut contohnya.

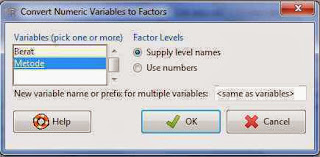
- Konversi data ke Factor. Tujuannya yaitu Memberi nama ketegori untuk metode dan umur tadi. Caranya pilih Data kemudian pilih manage variables in active data set dan klik convert numeric variables to factors. Kemudian akan muncul seperti berikut.

- Pilih metode dan pada factor level pilih supply level names. Kemudian Isi data seperti berikut.
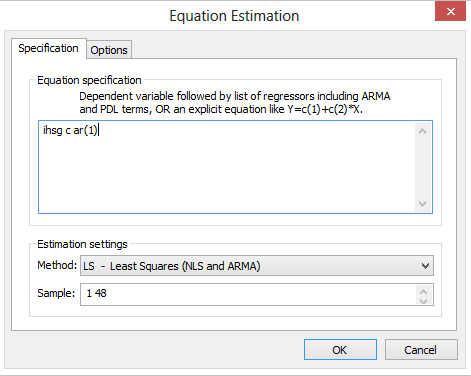
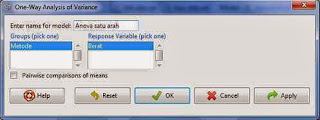
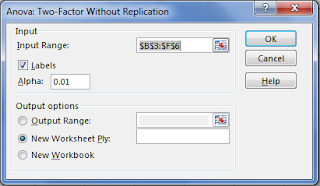
- Ke intinya. pilih Statistics kemudian pilih means dan klik Anova two way. Maka akan muncul tampilan berikut.

- blok semua variabel seperti pada gambar diatas. kemudian klik ok. maka outputnya sebagai berikut..

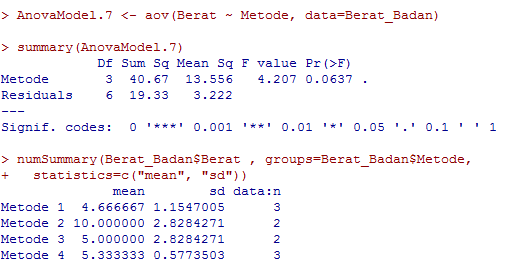
Intrepretasi Hasil uji anova satu arah dengan menggunakan R commander
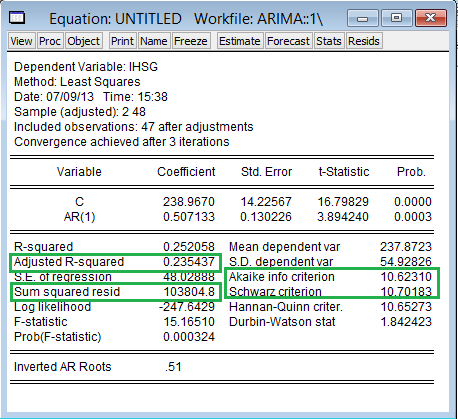
Anova Table
Pada bagian tersebut menjelaskan tabel anova. untuk bagian 'Metode:umur' menjelaskan interaksi pada tabel anova. Yang perlu diperhatikan kolom terakhir yaitu Pr(>F). Disini terdapat ada 3 nilai yang digunakan untuk menjawab hipotesis diatas. jika nilainya lebih besar dari 0.05(alpha) maka keputusan tolak H0. sebaliknya jika nilai besar dari 0.05(alpha) maka keputusan terima H0. dari 3 nilai p-value terdapat dua yang lebih besar dari 0.05(alpha) sehingga keputusan terdapat 2 terima h0. sedangkan yang satunya kecil 0.05(alpha) sehingga keputusan tolak h0.Berdasarkan hasil tersebut dapat diputuskan,
Perhitungan menunjukkan bahwa rata-rata penurunan berat badan pada Baris [Kel. Umur] dan Interaksi tidak berbeda [masih dianggap sama] hal ini terlihat dari nilai dari p-value yang lebih besar 0.05(alpha) sedangkan rata-rata penurunan berat badan dalam Kolom [metode diet] dapat dikatakan berbeda karena p-value yang lebih kecil 0.05(alpha).Bagi yang pengen liat langkah-langkah secara manual atau penjelasan materinya silahkan ke link berikut secara manual Atau mau membandingkan dengan tutorial anova dua arah dengan microsoft excel bisa kesini