Asumsi regresi yang akan dibahas kali ini adalah
heteroskedastis. setelah sebelumnya membahas
autokorelasi. heteroskedastis merupakan salah satu dari asumsi regresi yang menetukan dalam keberlanjutan analisis ini. supaya analisis regresi bisa dilanjutkan maka datanya harus tidak mengandung unsur heteroskedastis atau bisa disebut homoskedastis. Heteroskedastis berarti varians error bersyarat X merupakan angka yg tidak konstan.
heteroskedastis banyak ditemui pada data
cross-section, karena pengamatan dilakukan pada individu yang berbeda pada saat yang sama,
contoh kasus heteroskedastis
hubungan antara pendapatan dan menabung. orang berpendapatan rendah, tentunya mempunyai variasi yang rendah dalam menggunakan pendaptannya untuk menabung atau konsumsi. orang berpendapatan tinggi yang boros, tentu akan mempunyai konsumsi tinggi, dan tabungan yang lebih rendah dibandingkan orang yang tidak boros.
heteroskedastis tidak hanya terjadi pada data cross section, data
time series juga bisa terkena heteroskedastis.
contoh kasus heteroskedastis pada data time series
Perusahaan yang baru muncul, tentunya akan mempunyai produk yang relatif rendah pada saat pengenalan produk tersebut. ketika produksi masih sedikit, perusahaan tentunya tidak akan terjadi fluktuasi produksi besar, tetapi ketika produksi besar tentu akan memiliki fluktuasi yang besar. hal ini terjadinya karena adanya faktor pesaing, kondisi perekonomian dan sebagainya.
Berikut ilustrasi dengan gambar!
Penyebab heteroskedastis atau varians ui tidak konstan:
1. Sejalan proses belajar (the error-learning models) manusia, kesalahan (error) perilaku makin mengecilseiring berjalannya waktu. Dalam kasus ini, varians akan mengecil.
2. Dengan income meningkat, orang lebih mempunyai kebebasan dan lebih banyak pilihan utk penggunakan income-nya.Sehingga varians akan meningkat sejalan dengan peningkatan income.
3. Perbaikan teknik pengumpulan data akan menurunkan varians.
4. Kesalahan spesifikasi model:
• Kesalahan spesifikasi model yg dikarenakan menghilangkan variable penting dlm model.
• Dlm fungsi demand bila tidak dimasukan harga komoditi complementary sehingga varians tidak konstan.
• Kesalahan tranformasi data (mis. Rasio / first diff)
• Kesalahan bentuk fungsi (mis. Linier vs log-linier model).
Setelah sebelumnya kita sudah mengetahui apa dan penyebab heteroskedastis, maka selajutnya adalah. konsekuensi heteroskedastis itu sendiri kenapa begitu penting untuk diperhatikan.
1. Penaksir
OLS tetap tak bias dan konsisten, namun penaksir tsb tidak lagi efisien baik dalam sampel kecil maupun sampel besar (secara asimtotik)
2. Jika tetap menggunakan penaksir OLS pada kondisi heteroskedastis, maka varian penaksir parameter koefisien regresi akan
underestimate (menaksir terlalu rendah) atau overestimate (menaksir terlalu tinggi)Mendeteksi heteroskedastis
pastilah sangat perlukan, sehingga dapat mengetahui apakah mengandung hetero atau tidak. mendeteksi heteroskedastis ini diabgi dalam dua jenis yaitu secara grafik dan formal:
1. Metode Grafik
Dalam grafik ini, plot yang dibandingkan yaitu antara error kuadrat dengan variabel tersebut. sesuai dengan gambar diatas.pada gambar (a) terlihat bahwa errornya relatif konstan sehingga tidak menunjukkan pola pada varians. artinya gambar (a) homoskedastis sedangkan gambar (b),(c),(d), dan (e) menunjukkan pola masing-masing yaitu fluktuasi, trend,dan logaritma sehingga gambar tersebut heteroskedastis.
2. Uji formal
a. Uji park
Menggunakan fungsi:

karena varians umumnya tidak diketahui, maka Park menyarankan untuk menggunakan error sehingga persamaan regresinya menjadi

kesimpulan:Jika koefisien regresi (β) signifikan secara statistik, maka dikatakan terjadi heteroskedastisitas
b. Pengujian korelasi rank Spearman

dimana di = selisih rank dari 2 karakteristik yg berbeda
Langkah-langkah:
1.
Cocokan regresi Y terhadap X, dan hitung ei.
2.
Hitung rank dari |ei| dan Xi, selanjutnya hitung korelasi Spearman
Uji hipotesis:
H0 = terjadi homoskedastisitas
H1 = terjadi heteroskedastisitas
Gunakan statistik uji berikut:

Tolak H0 (terjadi Heteroskedastisitas) jika t hitung >
nilai kritis tabel t dengan derajat bebas n-2
c. Uji Goldfeld – Quandt
Langkah-langkah:
a.
Urutkan nilai X dari kecil ke besar
b.
Abaikan beberapa pengamatan sekitar median,
katakanlah sebanyak c pengamatan. Sisanya, masih ada
(N – c) pengamatan
c.
Lakukan regresi pada pengamatan 1, dan hitung SSE 1
d.
Lakukan regresi pada pengamatan 2 dan hitung SSE 2
e.
Hitung df = jumlah pengamatan dikurangi jumlah
parameter
Statistik Uji:

H0: Terjadi Homoskedastis
H1: Terjadi Heteroskedastis
Bila lamda > F tabel, kita tolak hipotesis nol yang mengatakan data mempunyai varian yang homoskedastis
d. Uji Breusch-pagan-godfrey
langkah-langkah:
1. Buat hipotesis
H0: varian ui homoskedastis
H1: lainnya
2. Estimasi model regresi, dan cari Ui.
3. Cari:
s2 =∑ µi 2/n
4. Hitung Pi dengan formula:
Pi = µi 2/s2
5. Regresikan pi dengan sehingga menjadi
Pi 2 = g0+g1Z1i+g1Z1i+…+gmZmi+Vi
6. Hitung Sum of square Regression(SSR) dan cari:
Q = ½ SSR
7. Bandingkan dengan tabel Chi-square dengan derajat bebas (m-1).
jika
Q> c2(m-1)maka keputusan terima ho atau
homoskedastis.e. Uji White (white's general heteroskedastis )
Dalam implementasinya, model ini relatif lebih mudah dibandingkan dengan uji-uji lainnya. perhatikan persamaan regresi berikut:
Yi =β1+β2X2i +β3X3i +ui
Langkah-langkah selanjutnya:
1. tentukan nilai error kuadrat masing-masing(Ui)
2. Buat persamaan
ui2 =α1+α2X2i +α3X3i+α4X2i 2+α5X3i 2 +α6X2iX3i +vi
3. Hipotesis
H0:homoskedastis
H1:Heteroskedastis
Statistik uji yang digunakan adalah:
n R2 ~ c2
4.Jika Nilai penghitungan
melebihi nilai kritis, diputuskan bahwa tidak terdapat
heteroskedastis.Metode ini bisa digunakan dengan
Eviews secara langsung namun untuk
SPSS belom terdapat.
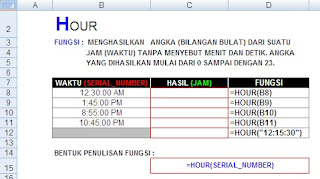































 dimana di = selisih rank dari 2 karakteristik yg berbeda
dimana di = selisih rank dari 2 karakteristik yg berbeda
