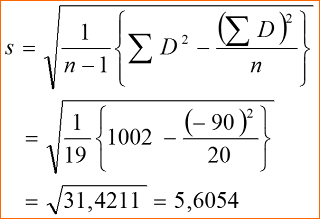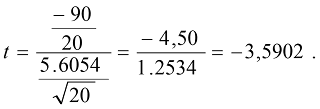Contoh Kasus dalam perhitungan Analysis of Variance (Anova) satu arah
Contoh Kasus Anova satu arah:
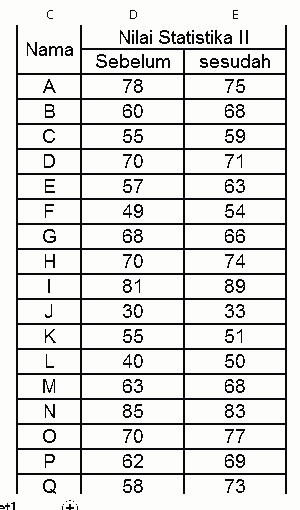
Terdapat 4 metode diet dan 3 golongan usia peserta program diet Berikut data rata-rata penurunan berat peserta keempat metode dalam tiga kelompok umur.| Sampel | Penurunan Berat Badan (Kg) | |||
| Metode 1 | Metode 2 | Metode 3 | Metode 4 | |
| Sampel 1 | 4 | 8 | 7 | 6 |
| Sampel 2 | 6 | 12 | 3 | 5 |
| Sampel 3 | 4 | - | - | 5 |
Uji pendapat tersebut dengan taraf nyata 5 %
Solusi kasus Anova satu arah
Identifikasi Metode statistik yang digunakan
Pertama. berdasarkan hipotesis yang digunakan yaitu membandingkan rata-rata lebih dari dua kelompok maka metode yang mungkin adalah Anova. kedua Sampel yang digunakan tiap kelompok berbeda perlakuan sehingga tipe anova yang cocok adalah Anova satu arah.
Dalam metode anova yang perlu diperhatikan ada empat. asumsi normal dan homogenitas antar varians kelompok harus terpenuhi. dalam contoh ini kita asumsikan asumsi terpenuhi karena kita fokus pada langkah-langkah anova satu arah. kemudian kelompok yang dianalisis berasal dari kelompok saling bebas. dan data yang digunakan merupakan data rasio. Setelah asumsi ini terpenuhi maka bisa lanjut ke perhitungan selanjutnya. kalau tidak ganti metode.
Langkah-langkah dalam uji hipotesis anova satu arah (one way)
- Masukkan/import data ke SPSS, Caranya yaitu buat dua kolom. Kolom pertama berisikan nilai dari semua data yang digunakan. kemudian kolom kedua berisikan pengelompokkan dari kolom pertama. jadinya hanya berisis angka yang menyatakan kelompok. Untuk jelasnya lihat gambar berikut.

- Menentukkan nama kategorik, langkah ini digunakan untuk mengkategorisasikan dari kolom dua tadi. karena hanya berupa angka oleh karena itu perlu diberi nama. agar pada output/hasil nanti lebih jelas. caranya pada variabel view (pojok kiri bawah). pada kolom value untuk variabel kategorik dklik maka akan muncul tampilan seperti berikut.

- Kemudian isi kan seperti pada gambar diatas. Pilih analyze, klik compare means dan pilih anova one way. Maka akan muncul tampilan seperti berikut. Bagian dependent List diisi dengan variabel Berat badan (berupa data kategorik) dan Factor diisi dengan Metode (data kualitatif). Untuk bagian post hoc digunakan untuk uji lanjutan yaitu digunakan untuk mengetahui kelompok yang mengalami perbedaan jika kesimpulan tolak H0. caranya aktifkan Bonferroni dan Turkey.

- Pada bagian Options, aktifkan descriptives dan Homogeneity of varians. Setelah itu pilih Ok. maka akan muncul output seperti berikut.

Intrepretasi hasil anova satu arah dengan SPSS
- Descriptive
Bagian ini memberikan informasi mengenai deskripsi dari tiap kelompok dan total. deskripsi ini mencakup banyaknya data (N), rata-rata(mean), standar Devisi, Standar error, Interval kepercayaan dari rata-rata(confidence interval) dan nilai minimum serta maksimum. - Test of Homogeneity of variances
uji yang digunakan dalam uji homogenitas varians pada spss yaitu uji levente. Perlu diperhatikan p value (sig). jika p value (sig) lebih besar dari 0.05(alpha) maka keputusan terima H0 yang artinya setiap kelompok homogen /sama. sebaliknya jika nilainya lebih kecil dari 0.05(alpha) maka keputusan tolak H0 artinya terdapat perbedaan varians antar kelompok minimal dua kelompok. Pada hasil diatas terlihat bahwa tolak H0. artinya terdapat perbedaan varians antar kelompok minimal dua kelompok. Pada anova perlu asumsi homogenitas varians. sehingga uji anova ini tidak bisa dilanjutkan lagi tapi karena ini hanya contoh anova kita abaikan saja. kita anggap varians sama. - Anova
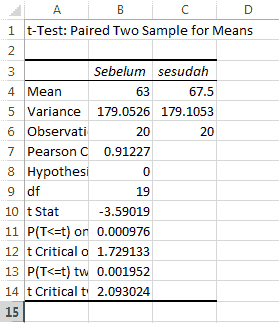
Bagian ini menampilkan tabel anova seperti pada materi anova satu arah. yang perlu dilihat pada bagian ini adalah P value. jika nilai p value lebih besar dari 0.05(alpha) maka keputusan terima H0 artinya tidak ada perbedaan rata-rata tiap kelompok.
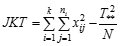
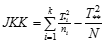
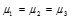 (Setiap metode memberikan rata-rata penurunan berat badan yang sama)
(Setiap metode memberikan rata-rata penurunan berat badan yang sama)
 Uji Bartlett digunakan untuk menguji apakah k sampel berasal dari populasi dengan varians yang sama. k sampel bisa berapa saja. karena biasanya uji bartlett digunakan untuk menguji sampel/kelompok yang lebih dari 2. Varians yang sama di seluruh sampel disebut homoscedasticity atau homogenitas varians. Uji bartlett pertama kali diperkenalkan oleh M. S. Bartlett (1937). Uji bartlett diperlukan dalam beberapa uji statistik seperti
Uji Bartlett digunakan untuk menguji apakah k sampel berasal dari populasi dengan varians yang sama. k sampel bisa berapa saja. karena biasanya uji bartlett digunakan untuk menguji sampel/kelompok yang lebih dari 2. Varians yang sama di seluruh sampel disebut homoscedasticity atau homogenitas varians. Uji bartlett pertama kali diperkenalkan oleh M. S. Bartlett (1937). Uji bartlett diperlukan dalam beberapa uji statistik seperti  (Homogen)
(Homogen)
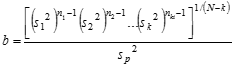

 (Homogen)
(Homogen).jpg) Analisis varians (analysis of variance, ANOVA) adalah suatu metode analisis statistika yang termasuk ke dalam cabang statistika inferensi. Dalam literatur Indonesia metode ini dikenal dengan berbagai nama lain, seperti
Analisis varians (analysis of variance, ANOVA) adalah suatu metode analisis statistika yang termasuk ke dalam cabang statistika inferensi. Dalam literatur Indonesia metode ini dikenal dengan berbagai nama lain, seperti