[Tutorial Excel] uji t Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik

Sampel berpasangan (paired sample) adalah sebuah sampel/kelompok dengan subjek yang sama namun mengalami dua perlakuan atau pengukuran yang berbeda. Seperti seseorang salesman yang bekerja, yang sebelumnya tanpa mendapatkan training, dengan sesudah ia mendapat training, bagaimana efektifitas training tersebut terhadap kemampuan menjualnya, apakah ada peningkatan atau tidak. Sampelnya tetap salesman yang sama tetapi mendapatkan dua perlakuan berbeda, yaitu kondisi sebelum dan kondisi sesudah training. Sebenanya materi Uji dua sampel berpasangan sudah dibuat. Pengantar diatas itu sedikit mengingatkan. Untuk kali tutorialnya menggunakan software Excel. Contoh kasus yang digunakan sama pada materi uji dua sampel berpasangan. Berikut soalnya.

Suatu kegiatan penelitian eksperimental, telah berhasil menemukan metode “ABG” sebagai metode baru untuk mengajarkan mata kuliah Statistika II. Dalam rangka uji coba terhadap efektifitas atau keampuhan metode baru itu, dilaksanakan penelitian lanjutan dengan mengajukan Hipotesis Nol (awal) yang mengatakan : Tidak terdapat perbedaan yang signifikan nilai Statistika II antara sebelum dan sesudah di terapkannya metode “ABG” sebagai metode mengajar mahasiswa UIB sem 6. Dalam rangka pengujian ini diambil sampel sebanyak 20 mahasiswa. Gunakan taraf kepercayaan 95 % (alfa=5% ) untuk menguji pernyataan (Hipotesis) tersebut.

Datanya Sebagai berikut:

Nama	Nilai Statistika II
	Sebelum	Sesudah
A	78	75
B	60	68
C	55	59
D	70	71
E	57	63
F	49	54
G	68	66
H	70	74
I	81	89
J	30	33
K	55	51
L	40	50
M	63	68
N	85	83
O	70	77
P	62	69
Q	58	73
R	65	65
S	75	76
T	69	86

Langkah awal dalam identifikasi uji t Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik

1. Dari permasalahan kasus terlihat bahwa peneliti ingin membandingkan pengaruh metode ABG Sebelum dan sesudah. tentu saja ini membandingkan satu kelompok tapi dengan dua perlakuan yang berbeda yaitu sebelum dan sesudah. sehingga uji kelompok berpasangan.
2. Perlu diperhatikan lagi yaitu hipotesisnya. pada soal terdapat pertanyaan penelitian yaitu apakah terdapat perbedaaan artinya disini kita menggunakan uji dua arah.
   
   
   
3. kemudian kita identifikasi apakah datanya parametrik atau tidak. bisa dilihat disini syarat parametrik. jika parametrik bisa pakai cara ini. tapi jika tidak memenuhi kita bisa menggunakan uji perbandingan rata-rata dua kelompok non parametrik. Kita asumsikan memenuhi asumsi Parametrik.

Langkah-langkah dalam uji t Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik dengan menggunakan Excel

1. Memasukkan/import data ke excel. Masukkan data seperti pada gambar dibawah ini.
   
   
   
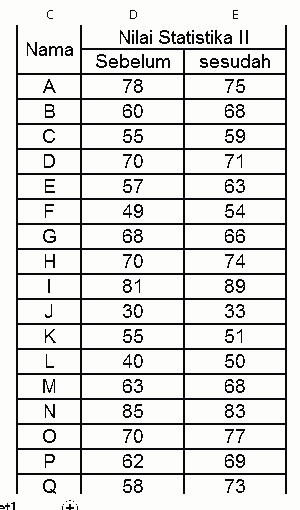
2. Kemudian Pilih Data, terus klik Data Analysis. Nah Data Analysis ini tidak muncul default di excel. untuk itu perlu menampilkannya terlebih dahulu.  Untuk langkah-langkah mengaktifkan toolpak silahkan klik toolpak analysis. Maka hasilnya seperti berikut ini.
   
   
   
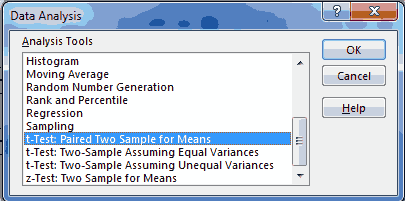
3. Setelah itu pilih paired two sample for means. Kemudian akan muncul Jendela seperti berikut ini:
   
   
   
4. Isil input dengan klik tanda panah kemudian pilih data mulai dari Nama variabel(Sebelum dan Sesudah) sampai data terakhir. Hypothesized mean defference dengan 0(nol). Kemudian Alpha dengan alpha pada soal yaitu 0.05. Kemudian Output Sesuai dengan keinginan.lalu klik OK.
   

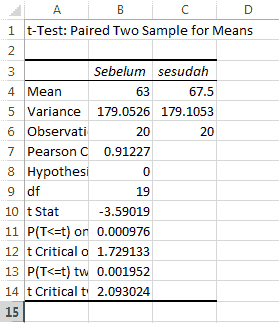
Intrepretasi Hasil output Excel Pada uji t Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik

• Rata-rata ketika sebelum menggunakan Metode "ABG" yaitu 63 nilai statistik II. setelah menggunakan metode "ABG" menjadi 67.5. sehingga ada peningkatan secara deskriptfif.
• Hasil Varians tidak jauh berbeda yaitu sekitar 179. dan jumlah observasi sampel yang digunakan yaitu 20. dengan degree of freedom(df) yaitu 20-1 adalah 19.
• Selain itu ada deskriptif berupa korelasi pearson yaitu 0.91227 sehingga bisa dikatakan hubungan sangat erat.
• Berdasarkan hasil tersebut diketahui t stat -3.59019. Nilai yang diperoleh ini sama dengan pada Materi uji t berpasangan.
• Hipotesis yang digunakan yaitu hipotesis dua arah sehingga menggunakan two tail. hasilnya t tabel yaitu 2.093024 dengan p value sebesar 0.001952. oleh karena  p value lebih kecil dari alfa 5% atau dengan melihat |t hitung| > t tabel maka keputusannya Tolak H0.
•  Ho ditolak , sehingga disimpulkan bahwa terdapat perbedaan yang signifikan antara hasil belajar statistika II sebelum dan sesudah diterapkannya Metode “ABG”.

Untuk materi tentang Pengujian Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik silahkan klik link tersebut.
Untuk Bisa membandingkan dengan software yang lain silahkan kesini:
[TUTORIAL SPSS] Uji T berpasangan 2 kelompok variabel numerik untuk parametrik
[Tutorial R] uji t Perbedaan Rata‐rata Dua kelompok berpasangan (dependent) parametrik


Sumber: pengalaman sendiri