Kapan menggunakan Analisis ragam (Anova) satu arah (one way)?
Anova digunakan untuk melihat perbandingan rata-rata beberapa kelompok biasanya lebih dari dua kelompok. Anova satu arah digunakan pada kelompok yang digunakan berasal dari sampel yang berbeda tiap kelompok. Jadi, bisa disimpulkan Pertama yang perlu dilihat tujuannya membandingkan rata-rata kelompok lebih dari dua. Kedua Sampel yang digunakan dari sampel yang berbeda per kelompok.
Asumsi-asumsi yang harus dipenuhi dalam analisis varians (anova):
- Data berdistribusi normal, karena pengujiannya menggunakan uji F-Snedecor
- Varians atau ragamnya homogen, dikenal sebagai homoskedastisitas, karena hanya digunakan satu penduga (estimate) untuk varians dalam contoh
- Masing-masing contoh saling bebas, yang harus dapat diatur dengan perancangan percobaan yang tepat
- Komponen-komponen dalam modelnya bersifat aditif (saling menjumlah).
Hipotesis dalam Anova (analysis of variance):
Dalam analysis of variance hanya satu hipotesis yang digunakan yaitu hipotesis dua arah (two tail). artinya hipotesis ini yaitu apakah ada perbedaan rata-rata. kita cuma pengen tahu itu, tidak spesifik yang mana yang berbeda. Nah kalau mau tahu kelompok yang benar-benar terdapat perbedaan rata-rata ada uji lanjutan dilakukan uji lanjutan. kalau tentang itu akan dibahas di lain tempat. Berikut hipotesis dalam Anova.
H0: μ1 = μ2 = μ3 = ... = μn, Tidak ada perbedaan yang nyata antara rata-rata hitung dari n kelompok
H1: μ1 ≠ μ2 ≠ μ3 ≠ ... ≠ μn, Ada perbedaan yang nyata antara rata-rata hitung dari n kelompok
Langkah-langkah melakukan uji hipotesis dengan ANOVA
Kumpulkan sampel dan kelompokkan berdasarkan kategori tertentu.
Untuk memudahkan pengelompokkan dan perhitungan, buat tabel data sesuai dengan kategori berisi sampel dan kuadrat dari sampel tersebut. Hitung pula total dari sampel dan kuadrat sampel tiap kelompok. Selain itu, tentukan pula hipotesis nol (H0) dan hipotesis alternatif (H1).Menentukan tipe anova
Untuk menentukan tipe anova. terlebih dahulu bertanya apakah dari hipotesis tersebut cocok untuk anova? jika tujuannya membandingkan rata-rata tiga kelompok atau lebih maka boleh pakai Anova. Pertanyaan kedua apakah sampel tiap kelompok diambil dari sampel yang berbeda? jika berasal dari sampel yang berbeda maka menggunakan Anova satu arah/one way.Memeriksa apakah sudah memenuhi asumsi-asumsi sehingga bisa digunakan anova
Normalitas,
adalah Menguji apakah data tiap kelompok memiliki distribusi normal. hal ini bisa dilakukan dengan uji kolmogorov smirnov, shapira wilk.Homogenitas
adalah Menguji apakah varians tiap kelompok sama. Dalam menghitung homogenitas bisa digunakan uji bartlett dan uji levene.Saling bebas
Menunjukkan bahwa setiap kelompok tidak saling berhubungan. Biasanya yang digunakan logika apakah saling bebas atau tidak.Aditif (Saling menjumlahkan).
Artinya data yang dianalisis merupakan data interval/rasio
Menghitung variabilitas dari seluruh sampel.
Pengukuran total variabilitas atas data dapat dikelompokkan menjadi tiga bagian, berikut rumus dalam Anova:Total of sum squares (SSt) – jumlah kuadrat total (jkt).
Merupakan jumlah kuadrat selisih antara skor individual dengan rata-rata totalnya.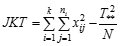
Keterangan: k = banyaknya kolom N = Banyaknya pengamatan/ keseluruhan data
ni = banyaknya ulangan di kolom ke-i xij = data pada kolom ke-i ulangan ke-j T** = Total (jumlah) seluruh pengamatanSum Square Between(SSb) – jumlah kuadrat kolom (jkk).
Variansi rata-rata kelompok sampel terhadap rata-rata keseluruhannya. Variansi di sini lebih terpengaruh karena adanya perbedaan perlakuan antar kelompok.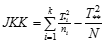 Keterangan
Keterangan
T*i = Total (jumlah) ulangan pada kolom ke-iSum Square within(SSw) – jumlah kuadrat galat (jkg).
Variansi yang ada dalam masing-masing kelompok. Banyaknya variansi akan tergantung pada banyaknya kelompok, dan variansi di sini tidak terpengaruh / tergantung oleh perbedaan perlakuan antar kelompok.JKG = JKT - JKK
Menghitung derajat kebebasan (degree of freedom).
Derajat kebebasan atau degree of freedom (dilambangkan dengan v, dof, atau db) dalam ANOVA akan sebanyak variabilitas. Oleh karena itu, ada tiga macam derajat kebebasan yang akan kita hitung:
Derajat kebebasan untuk JKT
merupakan derajat kebebasan dari Jumlah kuadrat total (JKT) ini akan kita lambangkan dengan dof JKT.db JKT = N - 1Derajat kebebasan untuk JKK
merupakan derajat kebebasan dari Jumlah kuadrat kolom (JKK) ini akan kita lambangkan dengan dof JKK.db JKK = k-1Derajat kebebasan untuk JKG
Merupakan derajat kebebasan dari Jumlah kuadrat galat (JKG) ini akan kita lambangkan dengan dof JKGdb JKG = N - k
Derajat kebebasan juga memiliki sifat hubungan yang sama dengan sifat hubungan variabel, yakni:db JKT = db JKK + db JKG
Menghitung variance antar kelompok dan variance dalam kelompok.
Variance dalam ANOVA, baik untuk antar kelompok maupun dalam kelompok sering disebut dengan kuadrat tengah atau deviasi rata-rata kuadrat (mean squared deviation) dan dilambangkan dengan MS atau KT. Dengan demikian, maka mean squared deviation masing-masing dapat dicari dengan rumus sebagai berikut:- KTK = JKK / db JKK
- KTG = JKG / db JKG
Menghitung F hitung
Menghitung nilai distribusi F (Fhitung) berdasarkan perbandingan variance antar kelompok dan variance dalam kelompok.Fhitung didapatkan dengan rumus di bawah ini:Fhitung = KTK/KTGMenghitung F tabel
Selain itu, F berdasarkan tabel (Ftabel) juga dihitung, berdasarkan nilai derajat kebebasan (langkah ke-4) menggunakan tabel distribusi-F. Jangan lupa untuk mencantumkan gambar posisi Fhitung dan Ftabel dalam grafik distribusi-F.Membandingkan Fhitung dengan Ftabel :
- Jika Fhitung > Ftabel : tolak H0
- Jika Fhitung ≤ Ftabel : terima H0
Buat kesimpulan,
sesuai dengan kasus awal yang ditanyakan. Simpulkan, apakah perlakuan (treatment) memiliki efek yang signifikan pada sampel data atau tidak. Jika hasil tidak signifikan, berarti seluruh rata-rata sampel adalah sama. Jika perlakuan menghasilkan efek yang signifikan, setidaknya satu dari rata-rata sampel berbeda dari rata-rata sampel yang lain.
Contoh penghitungan Analysis of variance (Anova) dengan tabel.
Berdasarkan langkah-langkah diatas untuk mempermudah perhitungan dibuat tabel seperti berikut:| Sumber Keragaman (SK) | Jumlah Kuadrat (JK) | Derajat Bebas (db) | Kuadrat Tengah (KT) | F hitung |
| Kolom (K) | 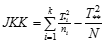 | db JKK = k-1 | KTK = JKK / db JKK | F hitung = KTK / KTG |
| Galat (G) | JKG = JKT - JKK | db JKG= N-k | KTG = JKG / db JKG | |
| Total (T) | 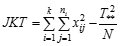 | db JKT= N-1 |
Contoh Kasus dalam perhitungan Analysis of Variance (Anova) satu arah
Contoh Kasus Anova satu arah:
Terdapat 4 metode diet dan 3 golongan usia peserta program diet Berikut data rata-rata penurunan berat peserta keempat metode dalam tiga kelompok umur.| Sampel | Penurunan Berat Badan (Kg) | |||
| Metode 1 | Metode 2 | Metode 3 | Metode 4 | |
| Sampel 1 | 4 | 8 | 7 | 6 |
| Sampel 2 | 6 | 12 | 3 | 5 |
| Sampel 3 | 4 | - | - | 5 |
Apakah keempat metode diet tersebut memberikan rata-rata penurunan berat badan yang sama?
Uji pendapat tersebut dengan taraf nyata 5 %
Solusi kasus Anova satu arah
Merumuskan Hipotesis
H0 :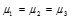 (Setiap metode memberikan rata-rata penurunan berat badan yang sama)
(Setiap metode memberikan rata-rata penurunan berat badan yang sama)
H1 : Ada suatu metode yang memberikan rata-rata penurunan berat badan yang tidak samaIdentifikasi model.
Pertama. berdasarkan hipotesis yang digunakan yaitu membandingkan rata-rata lebih dari dua kelompok maka metode yang mungkin adalah Anova. kedua Sampel yang digunakan tiap kelompok berbeda perlakuan sehingga tipe anova yang cocok adalah Anova satu arah.Memeriksa asumsi Anova.
Dalam metode anova yang perlu diperhatikan ada empat seperti pada keterangan diatas. asumsi normal dan homogenitas antar varians kelompok harus terpenuhi. dalam contoh ini kita asumsikan asumsi terpenuhi karena kita fokus pada langkah-langkah anova satu arah. kemudian kelompok yang dianalisis berasal dari kelompok saling bebas. dan data yang digunakan merupakan data rasio. Setelah asumsi ini terpenuhi maka bisa lanjut ke perhitungan selanjutnya. kalau tidak ganti metode.Menghitung F hitung melalui Variabilitas, Derajat bebas dan Kuadrat tengah
- Jumlah Kuadrat Total (JKT)
JKT = (42+62+42+82+122+72+32+62+52+52)-(602/10)=420-360=60 - Jumlah Kuadrat Kolom (JKK)
JKK=(142/3+202/2+102/2+162/3)-(602/10) =(65.33+200+50+85.33)-360 =40.67 - Jumlah Kuadrat Galat (JKG)
JKG = JKT - JKK = 60-40.67 = 19.33 - Kuadrat Tengah Kolom (KTK)
KTK = JKK / k-1 = 40.67/3 = 13.55 - Kuadrat Tengah Galat (KTG)
KTG = JKG / N - k = 19.33/6 = 3.22 - f hitung
f hitung =KTK / KTG = 13.55/3.22 = 4.21
- Jumlah Kuadrat Total (JKT)
Perhitungan Tabel anova
Agar mempermudah perhitungan kita menggunakan tabel berikut:Sumber Keragaman (SK) Jumlah Kuadrat (JK) Derajat Bebas (db) Kuadrat Tengah (KT) F hitung Kolom (K) JKK = 40.67 db JKK = 4-1 = 3 KTK =13.55 F hitung =
4.21Galat (G) JKG = 19.33 db JKG= 10-4=6 KTG =3.22 Total (T) JKT = 60 db JKT=10 -1 =9 Menghitung F tabel
F table pada α = 0.05 db1=3 dan dk2=6 adalah 4.76Kesimpulan :
Karena F hitung ada di daerah penerimaan (F hitung < F tabel) maka H0 terima, sehingga bisa disimpulkan setiap metode memberikan dampak rata-rata penurunan berat badan yang sama
No comments:
Post a Comment