Permasalahan dengan Data tidak normal: Penyebab dan strategi permasalahan

Data terdistribusi secara normal adalah konsep umum yang sering salah paham oleh beberapa orang. Beberapa orang percaya bahwa semua data yang dikumpulkan dan digunakan untuk analisis harus didistribusikan secara normal. Tapi distribusi normal tidak terjadi sesering orang pikirkan , dan itu bukan tujuan utama . Distribusi normal adalah sarana untuk mencapai tujuan , bukan tujuan itu sendiri .

Data terdistribusi secara normal diperlukan untuk menggunakan sejumlah alat statistik , seperti analisis regresi, analisis Cp / Cpk , uji-t, analisis varians ( ANOVA ) dan masih banyak lagi. Jika seorang praktisi tidak menggunakan alat khusus seperti itu, bagaimanapun , tidak penting apakah data terdistribusi secara normal . Distribusi menjadi masalah hanya ketika praktisi mencapai suatu titik dalam sebuah proyek di mana mereka ingin menggunakan alat statistik yang memerlukan data terdistribusi normal dan mereka tidak memilikinya .

Probabilitas plot pada Gambar di atas adalah contoh dari uji normalitas. Dalam hal ini , asumsi normalitas jelas tidak dapat terpenuhi, nilai p kurang dari 0,05 dan lebih dari 5 persen dari titik data berada di luar interval kepercayaan 95 persen .

Apa yang bisa dilakukan? Pada dasarnya, ada dua pilihan :

1. Mengidentifikasi dan, jika mungkin, menentukan alasan data tidak normal dan mengatasinya atau
2. Gunakan alat yang tidak memerlukan asumsi normalitas

Mengidentifikasi alasan data tidak normal

Ketika data tidak terdistribusi normal , penyebab non - normalitas harus ditentukan dan tindakan perbaikan yang tepat harus diambil . Ada enam alasan yang sering dialami untuk data tidak normal .

Alasan 1 : Data Ekstrim

Terlalu banyak nilai-nilai ekstrim dalam satu set data yang akan menghasilkan distribusi skewness(miring). Normalitas data dapat dicapai dengan menghilangkan data tersebut. Hal ini kemungkinan terjadi karena kesalahan menentukan pengukuran, kesalahan data-entry dan outlier dan untuk mengatasinya dengan menghapus data tersebut dari data yang digunakan untuk alasan yang masuk akal.

sangatlah penting bahwa outlier diidentifikasi sebagai penyebab yang benar-benar membuat data tidak normal sebelum mereka dieliminasi . Jangan lupa : Sifat data terdistribusi normal adalah bahwa kecil persentase dari nilai-nilai ekstrim yang diharapkan, tidak setiap outlier disebabkan oleh alasan khusus.

Alasan 2 : Tumpang tindih dari Dua atau Lebih Proses

Data tidak dapat terdistribusi secara normal karena sebenarnya berasal dari lebih dari satu proses , penjumlahan atau pergeseran, atau dari sebuah proses yang sering bergeser . Jika dua atau lebih set data yang terdistribusi secara normal yang tumpang tindih, data mungkin terlihat bimodal atau multimodal - itu akan memiliki dua atau lebih nilai yang paling sering terjadi.

Tindakan perbaikan untuk situasi ini adalah untuk menentukan X penyebab bimodal atau distribusi multimodal dan kemudian stratifikasi data . Data harus diperiksa lagi untuk normalitas dan setelah proses stratified dapat bekerja secara terpisah .

Gambar berikut menunjukkan data waktu akses website yang memiliki  data tidak normal pada sebuah website.

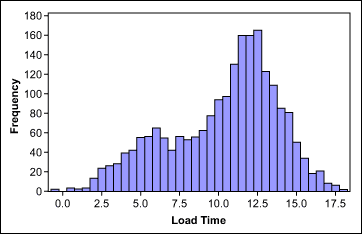
Setelah stratifikasi waktu akses website antara akhir pekan dibandingkan Data hari kerja, menunjukkan kedua kelompok berdistribusi normal. sehingga bisa dijadikan perimbangan dalam analisis data yang akan.

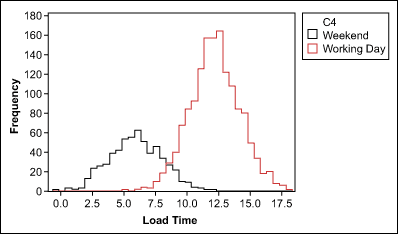
Alasan 3 : Kurangnya data Diskriminasi

Round- off error atau perangkat pengukuran dengan resolusi rendah dapat membuat benar-benar data continues dan data terdistribusi normal terlihat diskrit dan tidak normal . Kurangnya data diskriminasi dan karena terbatasnya jumlah nilai yang berbeda - dapat diatasi dengan menggunakan sistem pengukuran yang lebih akurat atau dengan mengumpulkan lebih banyak data.

Alasan 4 : Data yang diurutkan

Data yang dikumpulkan tidak mungkin terdistribusi normal jika itu merupakan hanya bagian dari seluruh data dalam suatu proses. Hal ini dapat terjadi jika data dikumpulkan dan dianalisis setelah penyortiran. Data pada Gambar dibawah diperoleh dari proses produksi botol di mana target adalah untuk menghasilkan botol dengan volume 100 ml . Spesifikasi minimal dan maksimal yang dapat diterima adalah 97,5 ml dan 102,5 ml dan di luar spesifikasi tersebut dihapus dari proses analisis. Sehingga terlihat pada gambar dibawah ini. Dari data tersebut tentunya data tidak terdistribusi normal karena hanya sebagian yang dimasukkan yaitu yang masuk dalam spesifikasi.

Alasan 5 : Nilai Mendekati Nol

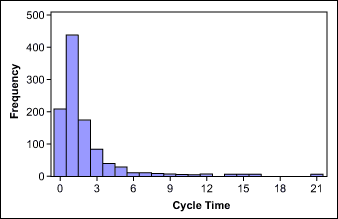
Jika proses memiliki banyak nilai mendekati nol, distribusi data akan miring (skewness) ke kanan atau kiri. Dalam hal ini, transformasi seperti tenaga transformasi Box - Cox, dapat membantu membuat data normal. Dalam metode ini , semua data dinaikkan , atau diubah , dengan eksponen tertentu , ditunjukkan dengan nilai Lambda . Ketika melakukan transformasi, semua data harus dilakukan perlakuan (diubah) yang sama.

Gambar di bawah ini menggambarkan contoh dari konsep ini. Gambar menunjukkan satu set data siklus - waktu;

menunjukkan data yang sama diubah setelah dilakukan transformasi dengan logaritma natural.

Untuk bahasan transformasi box cox silahkan ke link "transormasi box cox"

Perhatikan : Metode transformasi tidak memberikan jaminan distribusi normal . Selalu periksa dengan uji normalitas untuk menentukan apakah distribusi normal dapat diterpenuhi setelah transformasi .

Alasan 6 Data Mengikuti Distribusi Berbeda

Ada banyak tipe data yang mengikuti distribusi non-normal. Contoh berikut:

• Distribusi Weibull , ditemukan dengan data survival seperti waktu kelangsungan hidup suatu produk
• Distribusi log - normal, ditemukan dengan panjang data seperti ketinggian
• Distribusi Largest-extreme-value, ditemukan dengan data seperti waktu terpanjang down setiap hari
• Distribusi eksponensial, ditemukan dengan data pertumbuhan seperti pertumbuhan bakteri
• Distribusi Poisson, ditemukan dengan peristiwa langka seperti jumlah kecelakaan
• Distribusi binomial, ditemukan dengan " proporsi " data seperti persen barang cacat

Jika data berikut salah satu distribusi yang berbeda , harus ditangani dengan menggunakan alat dengan menggunakan disribusi yang sama.

Alat analisis yang tidak mensyaratkan data normal

Beberapa alat statistik tidak memerlukan data terdistribusi normal . Untuk membantu para praktisi memahami kapan dan bagaimana alat ini dapat digunakan , tabel di bawah ini menunjukkan perbandingan alat yang tidak memerlukan distribusi normal dengan setara - distribusi normal.

Perbandingan alat analisis untuk data berdistribusi normal dan tidak normal
Alat analisis yang menggunakan data normal	Alat analisis untuk data tidak normal	Distribusi yang diperlukan
T-test	Mann-Whitney test; Mood’s median test; Kruskal-Wallis test	Any
ANOVA	Mood’s median test; Kruskal-Wallis test	Any
uji t berpasangan	One-sample sign test	Any
F-test; Bartlett’s test	Levene’s test	Any
Analisis regresi	analisis regresi non parametrik	Any
Cp/Cpk analysis	Cp/Cpk analysis	Weibull; log-normal; largest extreme value; Poisson; exponential; binomial

Sumber : Dealing with Non-normal Data: Strategies and Tools